Equilibria of Dynamic Network Flows
A Brief Overview
Guest lecture at University of Augsburg, 21.11.2025
Lukas Graf, University of Passau
Equilibria in Non-Atomic Selfish Routing
Static Flows
Given: network $G=(V,E)$, source-sink pair $\source,\sink \in V$, set of $\source$,$\sink$-paths $\PathSet$,Given: traffic rate $r \in \IRnn$, edge-costs $c_e: \IRnn \to \IRnn$
static flow $f = (f_P)_{P \in \PathSet}$ with $\sum_{P \in \PathSet}f_P = r$ is (Wardrop) equilibrium if
\[\forall P,Q \in \PathSet: f_P \gt 0 \implies C_P(f) \leq C_Q(f)\]
Dynamic Flows
Given: network as above, traffic rate $r \in \rateSpace$, path-costs $C: \rateSpace^\PathSet \to C(\timeHorizon)^\PathSet, \class{tempstep a}{\data{tempstep-from=55}{f=(f_P)_{P\in\PathSet}}} \class{tempstep a}{\data{tempstep-from=56}{\mapsto (C_P(f))_{P \in \PathSet}}}$
dynamic flow $f=(f_P)_{P \in \PathSet}\in \rateSpace^\PathSet$ with $\sum_{P \in \PathSet}f_P = r$ is dynamic equilibrium if
\[\forall P,Q \in \PathSet \,\class{tempstep}{\data{tempstep-classes=59:hl}{\faa \theta \in \timeHorizon}}: f_P(\class{tempstep}{\data{tempstep-classes=59:hl}{\theta}}) \gt 0 \implies C_P(f)(\theta) \leq C_Q(f)(\class{tempstep}{\data{tempstep-classes=59:hl}{\theta}}).\]
Existence?
Properties?
Implementability?
Theorem: For any $r \in \rateSpace$ and any weak-strong continuous $C: \rateSpace^\PathSet \to \rateSpace^\PathSet$ there exists a dynamic equilibrium.
$f\in \rateSpace^\PathSet$ dynamic equilibrium if $\sum_P f_P = r$ and
\[\forall P,Q, \theta: f_P(\theta) \gt 0 \implies C_P(f)(\theta) \leq C_Q(f)(\theta) \tag{$\ast$}.\label{test}\]
Define
Fixed point exists by Kakutani-Fan-Glicksberg, since
- $K \coloneqq \set{ f \in \rateSpace^\PathSet \sMid \sum_{P \in \PathSet}f_P = r} \subseteq \rateSpace^\PathSet$
- $\Gamma(f) \coloneqq \set{ g \in K \sMid g \text{ satisfies } \eqref{test} \text{ wrt. } C(f)}$
Fixed point exists by Kakutani-Fan-Glicksberg, since
- $K$ non-empty, convex, compact wrt. weak topology
- $\Gamma(f)$ non-empty, convex
- $\Gamma$ has closed graph wrt. weak top. if $C$ is weak-strong continuous
Theorem (Brouwer's Fixed Point Theorem):
- $K \subseteq \IR^k$ non-empty, compact, convex
- $g: K \to K$ continuous
Theorem (Kakutani-Fan-Glicksberg Fixed Point Theorem, [AB06]):
- $V$ a locally convex Hausdorff space
- $K \subseteq V$ non-empty, compact, convex
- $\Gamma: K \to \PSet{K}$ has closed graph
- $\forall x \in K: \Gamma(x) \subseteq K$ non-empty, convex
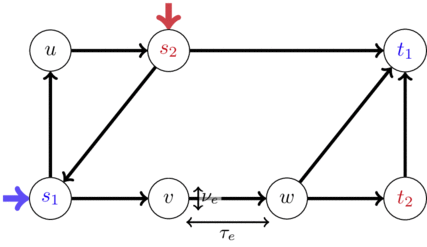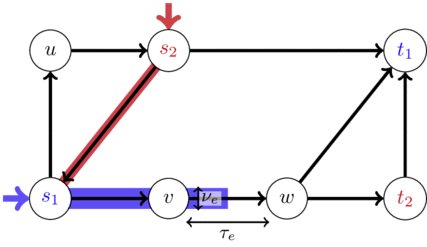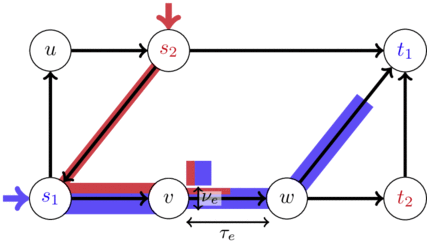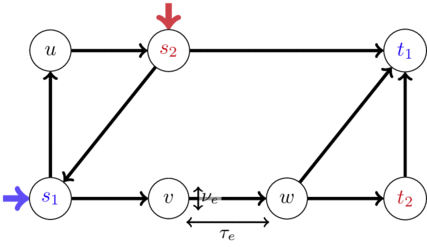
From now on: instantiate $C_P$ as travel times induced by Vickrey's deterministic queueing model ([V69]):
edge in-/outflow rates $f = (f_e^+,f_e^-) \in \rateSpace^{\{\pm\}}$ for edge $e \in E$ with
- free flow travel time $\tau_e \in \IRp$
- capacity $\nu_e \in \IRp$
- starts empty: $\ql(0)=0$
- works at capacity: $f_e^-(\theta+\tau_e) = \begin{cases}\nu_e , &\ql(\theta) \gt 0 \\ \min\set{f^+_e(\theta),\nu_e}, &\text{else}\end{cases}$
Lemma: Some properties of Vickrey flows:
- existence & uniqueness: $\forall f^+_e \, \exists! f^-_e$
- (weak-strong) continuity: $f^+_e \mapsto T_e$
- structure-preserving
- monotonicity
$\mapsto$
Thm.: $C: \rateSpace^\PathSet \to \rateSpace^\PathSet$ weak-strong continuous
Thm.: $\implies$ $\exists$ dynamic equilibrium
Thm.: $\implies$ $\exists$ dynamic equilibrium
Corollary: dynamic equilibria wrt. travel times induced by Vickrey queuing model exist.
$(f_P)$ dynamic equilibrium if
$\forall P,Q, \theta: f_P(\theta) \gt 0 \implies C_P(f)(\theta) \leq C_Q(f)(\theta)$
$\forall P,Q, \theta: f_P(\theta) \gt 0 \implies C_P(f)(\theta) \leq C_Q(f)(\theta)$
Lemma: $(f_P)$ is dynamic equilibrium (wrt. Vickrey) iff corresponding $(f^+_e,f^-_e)$ satisfies
and $\Theta_e \coloneqq \set{\theta \in \timeHorizon \sMid L_w(\theta) = A_e(L_v(\theta))}$
- or $\forall e=vw \in E, \faa \theta \in \timeHorizon: f^+_e(\theta) \gt 0 \implies \theta \in L_v(\Theta_e)$
- or $\forall e=vw \in E, \quad\forall \theta \in \timeHorizon: F^+_e(L_v(\theta)) = F^-_e(L_w(\theta))$
and $\Theta_e \coloneqq \set{\theta \in \timeHorizon \sMid L_w(\theta) = A_e(L_v(\theta))}$
Observation: $f$ dynamic equilibrium $\implies X_e(\theta) \coloneqq F^+_e(L_v(\theta))$ defines static $\source$,$\sink$-flow of value $\int_0^\theta r(\zeta)\diff\zeta$ (for every $\theta \in \timeHorizon$).
for right-constant $(f^+_e,f^-_e)_{e \in E}$ and any $\theta$ define
$x_e \coloneqq \rDeriv(F^+_e\circ L_v)(\theta)$ and $\ell_v \coloneqq \rDeriv L_v(\theta)$
Theorem ([KS11, CCL15, S20]): $f$ dynamic equilibrium iff for all $\theta \in \timeHorizon$ the vectors $(x_e) \in \IRnn^E$ and $(\ell_v) \in \IR^V$ satisfy:
\begin{align}
\class{tempstep a}{\data{tempstep-from=12}{(x_e)_{e \in E}}} &\class{tempstep a}{\data{tempstep-from=12}{\text{ is $\source$,$\sink$-flow of value } r(\theta)}} \\
\class{tempstep a}{\data{tempstep-from=13}{x_e}} &\class{tempstep a}{\data{tempstep-from=13}{\;= 0}} & \class{tempstep a}{\data{tempstep-from=13}{\text{ f.a. } e \in E \text{ with } \theta \notin \Theta_e}} \\
\class{tempstep a}{\data{tempstep-from=14}{\ell_w}} &\class{tempstep a}{\data{tempstep-from=16}{\;= \begin{cases}1, & w=s \\ \class{tempstep a}{\data{tempstep-from=17}{\min\set{\class{tempstep a}{\data{tempstep-from=18}{\rho_e(\ell_v,x_e)}} \sMid e=vw \text{ with } \theta \in \Theta_e},}} &\class{tempstep a}{\data{tempstep-from=17}{\text{else}}}\end{cases}}} & \class{tempstep a}{\data{tempstep-from=14}{\text{ f.a. } w \in V}} \\
\class{tempstep a}{\data{tempstep-from=24}{\ell_w}} &\class{tempstep a}{\data{tempstep-from=24}{\;= \rho(\ell_v,x_e)}} & \class{tempstep a}{\data{tempstep-from=24}{\text{ f.a. } e=vw \in E \text{ with } x_e \gt 0}}
\end{align}
where $\rho_e(\ell_v,x_e) \class{tempstep a}{\data{tempstep-from=22}{\;= \begin{cases} \frac{x_e}{\nu_e}, &\text{if } e=vw \text{ with } \ql(L_v(\theta)) \gt 0 \\ \max\set{\frac{x_e}{\nu_e},\ell_v}, &\text{if } e=vw \text{ with } \ql(L_v(\theta)) = 0 \end{cases}}}$ is derivative of $A_e(L_v(\theta))$.
$A_e(\zeta) = \zeta + T_e(\zeta) = \zeta + \frac{1}{\nu_e}\ql(\zeta) + \tau_e$
$\implies \rDeriv A_e(\zeta) = 1 + \frac{1}{\nu_e}\rDeriv\ql(\zeta)$
$\implies \rDeriv A_e(\zeta) = 1 + \frac{1}{\nu_e}\rDeriv\ql(\zeta)$
$\rDeriv \ql(\zeta) = \begin{cases}f^+_e(\zeta) - \nu_e, &\ql(\zeta) \gt 0 \\ \max\set{f^+_e(\zeta)-\nu_e,0}, &\text{else}\end{cases}$
↳ $(x,\ell)$ thin flow (with resetting)
Lemma: thin flows with resetting exist and are unique wrt. $\ell$.
Kakutani mmm
Now: $C_P =$ sum of travel times $T_e$ and edge tolls $p_e: \timeHorizon \to \IRnn$ ⤳ tolled equilibrium
Lemma ([RSVK25]): tolled equilibria are not unique (wrt. travel times)
Theorem ([GHS25a]): every dynamic flow without outflow from sink is
Theorem ([GHS25a]): implementable (=tolled equilibrium wrt. some tolls)
Theorem ([GHS25a]): implementable (=tolled equilibrium wrt. some tolls)
"Corollary" ([GHS25b]): socially optimal Vickrey flows are implementable.
monotonicity of Vickrey flows!
But for multi-commodity instances...
A network with
one flow without outflow from sinks
which is strictly better than
any flow with outflow from sinks
one flow without outflow from sinks
which is strictly better than
any flow with outflow from sinks
Theorem ([GHS25b]):
In multi-commodity instances
socially optimal flows are not always implementable.
socially optimal flows are not always implementable.
References/Further Reading
| [AB06] | Aliprantis, Border. Infinite Dimensional Analysis. A Hitchhiker’s Guide, 2006; DOI: 10.1007/3-540-29587-9 |
| [CCL15] | Cominetti, Correa, Larre. Dynamic Equilibria in Fluid Queueing Networks, OPRE, 2015; DOI: 10.1287/opre.2015.1348 |
| [CCO21a] | Cominetti, Correa, Olver. Long-Term Behavior of Dynamic Equilibria in Fluid Queuing Networks, OPRE, 2021; DOI: 10.1287/opre.2020.2081 |
| [CCO21b] | Correa, Cristi, Oosterwijk. On the Price of Anarchy for Flows over Time, MOOR, 2021; DOI: 10.1287/moor.2021.1173 |
| [GH24] | Graf, Harks. Dynamic Network Flows, lecture notes, 2024; available at https://git.fim.uni-passau.de/ |
| [GHS25a] | Graf, Harks, Schwarz. Tolls for Dynamic Equilibrium Flows, SODA, 2025; DOI: 10.1137/1.9781611978322.84 |
| [GHS25b] | Graf, Harks, Schwarz. Are System Optimal Dynamic Flows Implementable by Tolls?, EC, 2025; arXiv: arXiv:2503.07387 |
| [KS11] | Koch, Skutella. Nash Equilibria and the Price of Anarchy for Flows over Time, 2011; DOI: 10.1007/s00224-010-9299-y |
| [OSVK21] | Olver, Sering, Vargas Koch. Continuity, Uniqueness and Long-Term Behavior of Nash Flows Over Time, FOCS, 2021; DOI: 10.1109/FOCS52979.2021.00087 |
| [RSVK25] | Rosner, Schröder, Vargas Koch. Nash Flows Over Time with Tolls, WINE, 2025; arXiv: arXiv:2510.13518 |
| [S09] | Skutella. An Introduction to Network Flows over Time, 2009; DOI: 10.1007/978-3-540-76796-1_21 |
| [S20] | Sering. Nash flows over time, PhD Thesis, 2020; DOI: 10.14279/depositonce-10640 |
| [V69] | Vickrey. Congestion Theory and Transport Investment, 1969; available at: jstor.org/stable/1823678 |